A Working List of Probability Questions: Week 3

Programming, Statistics, and Past Interview Questions
July 6, 2020 | Updated August 5, 2020

Welcome to the last week of my trading interview prep series! My focus this week is to review programming and statistics concepts, along with exploring more challenging problems in areas I’ve already done practice problems in. Aside from these topics, I’ll mostly be pulling past interview questions from Glassdoor pages and Leetcode. As always, I’ll be providing solutions to the problems I do and a list of resources I use for reviewing concepts, along with a list of extra problems that I work on after this week is over.

Day Thirteen: July 6

Most of today’s problems are past interview questions in trading!

Problem 1. You have a drawer with an infinite number of two colors of socks, which exist in equal probability. What is the expected number of attempts at taking out socks individually from the drawer before a matching pair is found?
Solution. This is a past Jane Street interview question that should be answered without pen/paper. Note that a matching pair of socks must be found by the third draw by the pidgeonhole principle. After our first draw, we have probability $\frac{1}{2}$ of drawing the same color our second round and $\frac{1}{2}$ of drawing a different color. Should we draw a third color, it is guaranteed that we will complete a pair of matching socks the third round so we have and equal probability of completing the pair in two or three rounds. Then then expected number of attempts is $2.5$.

Problem 2. There is a raffle with 80 total tickets. Three tickets win a prize. I buy 5 tickets. What is the approximate probability that I win exactly one prize? Solution. We can approach this problem either combinatorially or by brute force (I prefer the combinatorial method but the brute force method is more intuitive). There are $\binom{3}{1}$ ways to choose one (and only one) of the three prizes. Of the remaining $77$ tickets, there are $\binom{77}{4}$ ways to choose four non-winning tickets. We can multiply these two together to get the number of outcomes in which we win only one prize. Finally, there are $\binom{80}{5}$ ways to choose $5$ tickets (winning or non-winning) so we divide our numerator by this to get the probability of getting a prize, or about $16.89\%$. To brute force it, let’s consider each of the three prizes. Note that the probability of winning the first prize is $\frac{5}{80}$. Then, considering that we can only win one of the three prizes,

Combining these probabilities gives us the same answer as above with our combinatorial solution.

Problem 3. Consider a deck with $26$ black and $26$ red cards. You draw one card at a time and you can choose either guess on whether it is red beforehand or simply observe the result. If the card is red you get $\$1$ and the game ends whenever you decide to guess. What is your strategy to play this game and the expected earnings? Solution. I have no idea what the right answer is so solving this question was rather fun. The most pedestrian strategy is to guess one the first card with probability $\frac{1}{2}$ of guessing correctly, with EV $\$0.50$. However, we can aim to slighly improve this by basing our future guesses on previously drawn cards. We can find the expected value guessing at any given round based on the number of red and black cards left in the deck. Let $f(r,b)$ be the expected payoff for the state where there are $r$ red and $b$ blue cards left. The probability of guessing correctly at any given state of red and black cards is $f(r,b) = \frac{r}{r+b}$ (the expected value of guessing at each round is also described by this function). This is where my strategy gets a bit more dicey: I’d first draw $5$ cards with the hope that I pick out more black cards than red cards which would increase the EV of the rest of the deck. Should I end up behind on this initial sequence of draws, I’m more likely to draw more black cards than red cards in the commin turns so I’ll continue to do so until I reacha bit over $50\%$ of drawing another red card. This is an inexact science and I don’t really have an answer to encapsulate every situation that could arise other than drawing more cards up to a point where there are few enough cards or high enough percentage of drawing a red card that I can maximize my probability of winning. This strategy introduces more variability into our expected payoff: instead of having a strictly $50\%$ chance of getting a dollar, we introduce a bit of rng into our draw. We can potentially go above or below $50\%$ of guessing a red card correctly. Doing this, I run the risk of never getting back up to $50\%$ should I draw $26$ red cards right off the bat (an extremely unlikely and unfortunate outcome). Update: I’ll be posting a revised answer to this question soon!

My calculation for the expected payoff is also a bit sketchy and relies on a symmetry argument: consider that we draw a sequence of cards such that we have probability $p$ of drawing a red card next time (EV $p$). However, we are just as likely to have draw the sequence of cards such that each $i^\text{th}$ card drawn in the second sequence is the opposite of its counterpart in our actual draw, giving EV $1-p$. Applying this to any state of cards that we decide to guess at, we are equally likely to have a payoff $p$ as a payoff $1-p$ so our expected value of the overall game is $\$0.50$ regardless of our strategy. All in all, I’m not really sure if I improve anything for myself by taking on increase variability but I am inclined to be less risk averse given that I cannot lose money.

Problem 4. How would I design the elevators for a new 40 story office building that had an average of 100 people per floor to most efficiently fill and empty the building given a standard 9-5 workday and traffic conditions in my city? The answer should to be as detailed as possible, including expected passengers per car, time per stop, average floors stops per trip at various hours, etc. Solution. This is a Google PM question but the nature of this question feels very trading-esque. Note hat $4000$ people must enter and exit the building each day, presumably during the morning and afternoon close to $9$ and $5$. Some people will enter in early and some will funnel in a bit later in the workday so I’ll asume we have some sort of normal distribution of people entering the office centered at $9:00$, with sd of $30$ minutes. Then, we have approximately the following number of people using the elevator in various times during the morning:

7:30 - 8:00 - $80$
8:00 - 8:30 - $560$
8:30 - 9:00 - $1360$
9:00 - 9:30 - $1360$
9:30 - 10:00 - $80$
10:00 - 10:30 - $80$

During lunch some people will probably leave the office, but it’s quite unlikely that the elevators will be operating at full capacity since some people (perhaps even a majority) will stay in for lunch. Let’s say that there are $10$ elevators and each elevator can carry an average of $10$ people, disregarding weight, so we have $1360$ people being funnelled into the building in a $30$ minute interval. Then each elevator should make $\frac{1360}{100} = 13.6$ trips between the first floor and carrying people up to higher floors. Since this office complex is relatively large, we should consider splitting up the floors serviced by each elevator so the time spent travelling is minimized. We can break this up so that each elevator services $8$ floors: elevator 1 & 2 servicing floors $1-8$, elevators 3 & 4 servicing floors $1, 9-16$, etc. Then each elevator makes an average of $9$ floor stops per trip, with the outlier of elevators $1,2$ which average $8$ floors per trip. While this helps reduce inefficiency, the elevators that travel the most should still travel between te first floor and the last $8$ floors, making an average of one trip per $2.2$ minutes. It takes relatively little time for people to exit an elevator, so we’ll allocate an average of $5$ seconds per stop before moving on to the next floor. Then elevators $9,10$ will spend $40$ seconds travelling between top floors, which gives them about $90$ more seconds to travel between floor 1 and floor 40 and fill up another elevator full of people. Note that this answer can be a bit more detailed, focusing in on maximizing the carriage capacity of higher floor elevators by making use of the fact that people on lower floors will take the stairs, and other random variables that I haven’t considered.

Problem 5. Consider a card game with two black cards and two red cards. You play a game where you draw a card each round. If it’s black you lose a dollar and if its red you win a dollar. You can choose to stop at any time. What’s your winning strategy and its associated expected value? Solution. Note that by playing the game out completely we ensure breaking even. To cover the obvious cases, if we finish the third draw with one dollar ($RBR$) or the second draw with two dollars ($RR$), it makes sense to end the game since we are guaranteed to lose part of our winnings by continuing. Also, if we’re behind at any stage of the game we continue drawing since we can guarantee an even outcome and if we’re even at any point in the game we should keep drawing since we will either have positive gains or play out the entire game and end even. Let’s consider what happens when we draw $R$ first. Then we will be up one dollar and have probability $\frac{1}{3}$ of drawing another red (net $+2$), $\frac{2}{3}\cdot \frac{1}{3} = \frac{1}{3}$ of drawing two blacks and forcing us to finish the game ($+0$), and $\frac{1}{3}$ of drawing $BR$ afterward and ending ($+1$). So conditional of drawing a red first turn, we have ev $\frac{1}{3} \cdot 2 + \frac{1}{3} \cdot 1$. Now consider rolling $B$ first: if you draw two consecutive reds afterwards ($\frac{1}{3}$) you can end with $\$1$ and break even otherwise ($\frac{2}{3}$). Then, our total EV is $\frac{1}{2} \cdot 1 + \frac{1}{2}(\frac{1}{3} \cdot 1 + \frac{2}{3} \cdot 0) = \frac{2}{3}$ using this strategy. This can be extended to any number of cards.

Day Fourteen: July 7

Todays problems are a mix of programming questions from Leetcode and some past trading interview questions.

Problem 1. Given a string, find the length of the longest substring without repeating characters. Solution. This is a leetcode medium question. We can solve this problem with a sliding window technique and minimize time complexity by using a hashmap, gicing an $O(n)$ solution. Starting from the first index of the string, we can insert each character into the hashmap and begin counting substrings sies through a counter variable. Should we happen to come across a non-unique character in our hashmap, we slide our “window” once index to the right and scan the next substring and update our counter variable each time we come across a unique character.

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        int left(0), counter(0);
        unordered_map<char, int> myMap;

        for (int i = 0; i < s.size(); i++) {
            if (myMap.find(s[i]) != myMap.end()) {
                left = std::max(left, myMap[s[i]] + 1);
            }
            myMap[s[i]] = i;
            counter = std::max(counter, i - left + 1);
        }
        return counter;
    }
};

This solution runs faster than $54\%$ C++ submissions so it could definitely be streamlined/improved. I implemented a basic sliding window technique and didn’t dedicate much time to improving it.

Problem 2. There are $3$ balls distributed in $4$ boxes. What is the probability that the maximum number of balls in any given box is exactly $2$? Solution. This is an incredibly simple combinatorics question that I got wrong on a recent HackerRank. The number of ways to arrange $n$ balls into $k$ boxes is $\binom{n+k-1}{n}$, so there are $\binom{6}{3} = 20$ ways to arrange the the balls into boxes. You can learn more about balls and boxes combinatorial methods here. To find the desired probability we will consider the case that $2$ balls are in one box. Then, the final ball is in one of the three remaining boxes. There are $\binom{4}{1}$ ways to pick a box to carry two balls and $\binom{3}{1}$ ways to pick which of the remaining boxes we place the last ball into for each $2$-balled box. Then, we have probability $\frac{\binom{4}{1} \binom{3}{1}}{\binom{6}{3}} = \frac{3}{5}$ of the given scenario occuring.

If you didn’t know the formula for the total number of ways to arrange the balls into boxes we can still derive it with combinatorial methods. There are three cases that we must consider: all balls are contained in different boxes, two balls are contained in one box and the final one in another box, and all three balls in one box. There are $\binom{4}{3}$ ways to choose three boxes for which each contains one ball, $\binom{4}{1}\binom{3}{1}$ ways to choose one box to hold two balls and a second box to hold the final ball (as previously calculated), and $\binom{4}{1}$ ways to choose one box to contain all the balls. Then our probability of obtaining the desired outcome is $\frac{\binom{4}{1}\binom{3}{1}}{\binom{4}{3} + \binom{4}{1}\binom{3}{1} + \binom{4}{1}} = \frac{3}{5}$.

Problem 3. You have a box filled with cash. Cash value is uniformly and randomly distributed from 0 to 1000. You are trying to win the box in an auction: you win the box if you bid at least the value of the cash in the box; you win nothing if you bid less (but you lose nothing). If you win the box, you can resell it for 150% of its value. How much should you bid to maximize the expected value of your profit (resale of box minus bid)? Solution. We would bid $\$0$ as the expected value of this game is always negative. I’ll assume that cash means there will not be fractions of a dollar in the box. Let $X$ be the payout of the box and $Y$ be the amount that we pay for the box after bidding. Then we have $P(X) = 1.5X - Y$, $X\leq Y$ as ur profit function. Since $\mathbb{E}[P(X)] = 1.5\mathbb{E}[X] - \mathbb{Y}$, we first need to find the expected value of $X$ and $Y$. Each integer between $0$ and $1000$ is equally likely to be in the box ($P(X=x)= \frac{1}{1001}$). Since we only realize the payout of the box if $X\leq Y$ we only need to sum up to $Y$:

To find the expected value of $Y$, note that we will pay $Y$ dollars for the box if $X\leq Y$ and $0$ otherwise. Given a $Y$, the probability that $X\leq Y$ is $\frac{Y+1}{1001}$ since each potential value of $X$ shy of $Y$ has probability $\frac{1}{1001}$. Then $\mathbb{E}[Y] = \frac{Y(Y+1)}{1001}$. It follows that

which is always negative so we should not bid any amount for the box. Our optimal bid then is $\$0$, with expected payoff $\$0$. Note that my original assumption was the impetus for using a summation; should I have assumed that any value was possible in the box, then we would have to approach $X$ as though it were a continuous variable.

Problem 4. Imagine I flip 100 coins in a sequence, and you need to guess the sequence in one try. You are allowed to ask one yes/no question. What do you ask to maximize the probability of guessing the sequence? Solution. This question is a bit open-ended as there isn’t really a definitive correct answer. Without information, we have probability $(\frac{1}{2})^{100}$ of guessing the entire sequence correctly. We can double our probablility to $(\frac{1}{2})^{99}$ by asking a question about any specific index in the sequence (we should ask for the first one since it is the only index that we are guaranteed to reach). We could potentially ask whether there are more heads than tails or vice versa, but the probability that one type of flip occurs more frequently than the other in the sequence is $\frac{1}{4}$ (convince yourself of this) and a yes to the question provides minimal benefit in choosing the values of any specific index until very late in the sequence. A no to the question, which is far more likely, means that the question is esentially wasted as we don’t know whther there are more tails than heads or if they are equal in number. Potentially we could ask about the second or the third index, which would give us probability $\frac{1}{2}, \frac{1}{4}$ of guessing the first two and three indicies respectively. However, this still leaves the first index up to chance and runs the risk of guessing no index correctly should we guess the first one wrong and the game ends. I can’t really think of any other ways to gather information that would be readily pertinent to guessing the the sequence and it seems like asking for the first index is the best option since we can guarantee at least one index is correct. Were I more confident in my understanding of the coin flips or the nature of the sequence I potentially would employ the more risky strategy of asking the identity of some non-first index, or even if the number of heads is greater than the number of tails if I were confident enough in my ability to guess more than $50\%$ of the sequence. As it stands however, asking about anything but the first index seems to be extremely high risk low reward.

Day Fifteen: July 8

Here are some more betting games from previous interviews.

Problem 1. You have all the clubs from a deck, 13 cards, and you can choose 2 from the deck and get paid their product, where all face cards are considered to be 0. You can pay $1$ to reveal the difference of any two cards you choose, how much would you pay to play this game?
Solution. Our probability of getting a nontrivial outcome (not picking a $J,Q,K$) just guessing off the top is $\frac{\binom{10}{2}}{\binom{13}{2}} = \frac{15}{26}$. We’ll aim to improve this and maximize our payout from this game. Let’s index our cards and call them $C_1, C_2, \dots, C_13$, with $C_i$ describing the $i^\text{th}$ card from the left. WOLOG lets make $C_1$ the card that we compare all other ones to. If $C_1$ is a face card, then there are $2$ more face cards within the next $12$ cards so it will take $11$ comparisons for us to encounter a second face card, at which we’ll see the difference between $C_1$ and the new face card is $0$. From there, we know that all of the previous comparisons we’ve done have yielded the exact value of each card, which allows us to select the $9$ and $10$ cards for a $\$90$ payout. Note that this is the worse case scenario and there is a chance we come across the second zero much earlier and it’s simply our imperative to find the $9,10$ cards through direct comparison.

If the first card is not a face card, then there are $3$ face cards in the next $12$ cards that we’ll compare to $C_1$. Then, within $11$ cards, we’ll come across at least $2$ face cards, at which we’ll realize that two of the comparisons that we’ve done yield the same difference between cards. The two cards that have the same difference when compared to $C_1$ are then face cards and their difference with $C_1$ is simply the value of $C_1$. From there, you can reverse engineer the values of the rest of the cards you went through in order to find the $9,10$ cards. Again, we might come across the case where this occurs much earlier than the $11^\text{th}$ comparsion which would mean that we’d simply have to find the $9,10$ cards again through comparisons. From these two cases, we’ve confirmed that spending $\$11$ can guarantee a payout of $\$90$. I’d then pay up to $\$79$ to play this game, which ensures that I’ll always have a nonnegative expectation. Note that $79$ is not the expected value of the game, as we’d have to consider the multitude of cases that can arise with the cards, but that’s relatively tedious to calculate so I’m inclined to pay up to, or maybe a bit more than, $\$79$. The reason I’m willing to go beyong $\$79$ is because paying that amount guarantees a nonnegative payout, but the expected profit of doing this is positive, as we’ve essentially done a worst case analysis and haven’t considered the game on average.

Problem 2. We randomly sample integers $a,b,c$ from a uniform distribution of $[0,1]$. What is the probability that $ax^2 + 2bx + c = 0$ has real roots? Solution. In order for the given quadratic equation to have real roots, we must have $4b^2 - 4ac \geq 0$, or $b^2 \geq ac$. This can be solved by finding the probability that $b^2 \geq ac$ on the unit cube, but I’m not particularly good at multivariable calculus so I opted for a solution using random variables. For a uniformly distributed r.v. $X$ on $[0,1]$, we have that $-\ln(X)$ follows an exponential distribution with $\lambda = 1$. Then, let $A,B,C$ be uniform independent random variables on $[0,1]$ and

for $X$ exponential and $Y$ with the pdf $xe^{-x}$ for $x>0$. Since $X$ and $Y$ are independent, we have

Then the probability that our quadratic equation has real roots is $\frac{5}{9}$. This solution relies on drawing the connection between the negative log of a uniform distribution on $[0,1]$ being exponential and the sum of exponential distributions with $\lambda$ parameter having a pdf of $\lambda^2 xe^{-\lambda x}$. A more basic case of this problem with $ax^2 + bx + c = 0$ can be found here.

Problem 3. Let’s play a game - I give you a 12 sided die and will pay you whatever the die lands on. If you are unhappy with the roll, you can choose to roll another two 6-sided dice and I will pay you the sum of the two dice. How much are you willing to pay to play this game? Solution. This is a Jane Street interview question that I came across on their Glassdoor page. Note that the expected value of the second dice is $7$ (just the sum of expected value of two fair dice) so if we roll less than a $7$ on the $12$-sided die, we’ll be incentivised to roll again. This occurs with probability $\frac{1}{2}$ so we have $\frac{1}{2}$ chance of getting a $\$7$ payoff. On the other hand, we also have $\frac{1}{2}$ probability that we roll at least a $7$, giving us expected payoff of $\frac{1}{6}(7 + 8 + 9 + 10 + 11 + 12) = 9.5$ for the scenario that we roll at least a $7$ of the $12$-sided die. Then, the total expected value is $\frac{1}{2} \cdot 7 + \frac{1}{2} \cdot 9.5 = 8.25$. Then it follows that I’d pay up to $\$8.25$ to play this game, assuming that I’m using the optimal strategy that I described above.

Problem 4. Given n non-negative integers $a_1, a_2, \dots, a_n$ , where each represents a point at coordinate $(i, a_i)$. n vertical lines are drawn such that the two endpoints of line $i$ is at $(i, a_i)$ and $(i, 0)$. Find two lines, which together with x-axis forms a container, such that the container contains the most water. Solution. This is another Leetcode medium question. The brute force solution involves comparing every possible pair of lines and the volumes of containers that they build, which run in $O(n)$ time. On the other hand, we can approach the question with the following intution: given two lines, the area of the container formed is limited by the height of the lower stick. In hopes of getting a taller line, we would shift the lower line one unit to the right (or left depending which is shorter), which will decrease the width but add the potential of increasing the height of the next line. After each iteration of line moving, we’ll check the area again and make updates to the maximum area should that be applicable. This is done as opposed to moving the taller line, which would decrease the width of the container and add no possibility of improved height. This method won’t always guarantee us a larger area, but it encompasses all the possibilites of higher sticks adding area as we “traverse” the array. This gives us the following solution:

class Solution {
public:
    int maxArea(vector<int>& height) {
        int size = height.size();
        int left = 0;  
        int right = size - 1;
        int maxArea = 0;
        
        while(left != right){
            maxArea = max(maxArea, containerArea(height[left], height[right], right - left));
            
            if(height[right] > height[left]){
                left++;
            }else{
                right--;
            }
        }
        return maxArea;
    }
    
    int containerArea(int lHeight, int rHeight, int width){
        return width * min(lHeight, rHeight);
    }
};

This solution runs in $O(n)$ time, but does waste some resources. When we shift over from one line to another, we’re doing it in hopes that we’ll compensate for the smaller width by getting to a higher line. We can guarantee that the next area we consider is with a stick of higher height by using a while loop to continue incrementing our line index until we reach a line that is taller than the original one we deemed was too short. This would be relatively simple to implement, simply changing left++ to while(height[left] <= min(height[left], height[right]) {left++;} (do this for right as well), which would make up for the wasted time we iterate through our origina while loop.

Day Sixteen: July 9

Here are a couple more solutions to some leetcode and past interview questions at trading firms.

Problem 1. What is the expected value of the largest of four dice rolls? Solution. This is a pretty straightforward order statistic question. Let $X_i$ be the random variable denoting the outcome of the $i^\text{th}$ dice rolls. Our goal is to find the pmf of $Z = \max\{X_1, X_2, X_3, X_4\}$, which is the $4^\text{th}$. One thing to keep in mind is that each of the four dice rolls is independent so we can multiply their probabilies together when combining cdf’s. Then,

Since each $X_i$ is discretely distributed, we have that $P(X_i = x) = P(X \leq x) - P(X \leq x-1)$ so $p_{Z}(z) = \frac{z^4 - (z-1)^4}{6^4}$. We can directly use this pmf to calculate the expected value of $Z$:

Then, the expected value of the largest of four independent dice rolls is $5.24$. Note that we can extend this problem to $n$ dice rolls by employing a similar strategy of using the definition of expected value and calculating the cdf of $Z = \max\{X_1 , \dots, X_n\}$, where $X_1, \dots X_n$ signify the outcomes of $n$ independent dice rolls.

Problem 2. If I toss 3 Tic Tacs on a tic-tac-toe board at random, and I pay you $\$20$ if the pieces create tic-tac-toe, and you pay me $\$1$ if they dont, do you want to play the game? Solution. This is a past interview question at SIG. My intuition led me to solve it combinatorially since it’s a varient of the ball and boxes question from a couple days ago. Assuming that Tic Tacs don’t have to land on unique boxes on the board, we have $\binom{9}{3} + \binom{9}{1}\binom{8}{1} + \binom{9}{1} = 165$ ways to arrange the Tic Tacs on the board (this can also be done by $\binom{9+3-1}{3}$). Additionally, there are $8$ ways to arrange the Tic Tacs in order to create a tic-tac-toe with the board (6 ways across the rows and columns and 2 additional for the diagonals). Then, our expected payout to this game is

Our expected payout from playing this game is about $2$ cents per turn so I would play this game. The original question on SIG’s Glassdoor page can be found here, and documents the scenario in which all the Tic Tacs land on unique boxes and the payout for a tic-tac-toe is only $9$ dollars instead of $20$.

Problem 3. Flip a fair coin many times until either a pattern of $HHT$ or $HTT$ occurs. What’s the probability that HHT occurs before HTT? Solution. This is a classic question that has a relatively elegant solution. We could potentially model this with a Markov chain but this approach is rather extensive and unnecessary. Note that since both sequences begin with $H$, sequences with leading tails can be ignored up until the appearance of the first $H$. Then within the first three flips, the following sequences each appear with probability $\frac{1}{4}$:

$HHH$: We will have $HHT$ appear first as soon as the next heads shows up $HHT$: $HHT$ appears first
$HTT$: $HTT$ appears first
$HTH$: The sequence is basically reset as $H$ is no longer within the most recent $3$-flip sequence

Note that we dont consider the $4$ outcomes that begin with a tail flipped first due to our earlier observation. The first two cases guarantee that $HHT$ will be flipped first, the third guarantees $HHT$ appears first, and the final case is a reset. Then $HHT$ appears first with probablity $\frac{2}{3}$, twice that of $HTT$ appearing first. You can find a similar question dealing with consecutive tennis wins here.

Problem 4. You roll a dice until you get a $5$. What is the expected value of the minimum value rolled? Solution. This is a past interview at Jane Street. It can be solved with the tail sum formula, $\mathbb{E}[x] = \sum_{x=0}^\infty P(X\geq x)$ but I approached it combinatorially. Let $X$ be the minimum value of the dice rolls until the first $5$ is rolled. The maximum value of $X$ is $5$ as rolling only $6$’s gets cancelled out when the first $5$ is rolled so $\mathbb{E}[X] = \sum_{x=1}^5 P(X = x)$. Consider $P(X=1)$: since $1$ is the smallest possible value for $X$ we don’t need to consider the values $2,3,4$ being rolled before the first $5$. We only need a $1$ to be rolled before the first $5$, which happens with probability $\frac{1}{2}$. For $P(X=2)$ we need $2$ to be rolled before $5$ and $1$ to not be rolled before $5$. If we consider the $3!$ unique permuations of $\{1,2,5\}$, there is only one of them ($251$) that satisfies this condition. Then, there is $\frac{1}{3!} = \frac{1}{6}$ chance that $P(X=2)$. For $P(X=3)$ we need $3$ to be rolled before $5$ and $2$ and $1$ to be rolled after $5$. Only $3512$ and $3521$ satisfy this giving probability $\frac{2}{4!} = \frac{1}{12}$. For $P(X=4)$ we need $4$ rolled before $5$ and $1,2,3$ rolled afterward, which has $\frac{3!}{5!}$ probability. Finally, for $P(X=5)$, we need to roll $5$ first, followed by $1,2,3,4$ in any order. This has $\frac{4!}{5!} = \frac{1}{5}$ probability, giving

Then the expected value of the minimum value of dice rolled is about $2.28$.

Day Seventeen: July 10

Today is the last day I’ll be consistently updating my website with new problems but stay tuned below for more resources in the future!

Problem 1. Suppose there are $n$ points on a circle. How many regions can be formed by connecting all of these points to one another? Solution. This is a problem that can solved for by studying the first few cases. Lets called $R(n)$ the number of regions that can be formed with $n$ points. Then $R(1)=1$ and $R(2)=2$. Let $R'(n)$ be our approximation of $R(n)$. On first glance, it seems like the recurring pattern is $R'(n) = 2^{n-1}$. However, this breaks down when 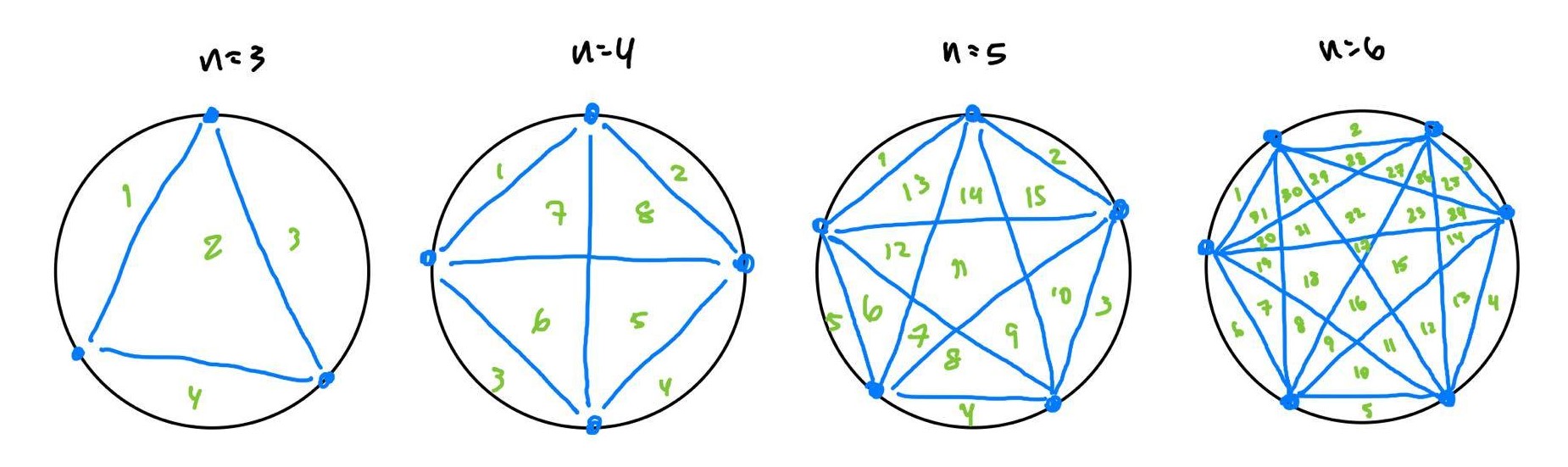$n=6$ as $R(6) = 31 \neq 32$. We can approach this problem instead by considering the number of regions that each new chord between points creates. For $n$ points, connecting each of them gives us $\binom{n}{2}$ chords. However, in the cases of $n=1, 2$ we have $\binom{n}{2} = 1, 2$ respectively while $R(1) = 1$ and $R(2) =2$. In both of these cases, there is an additional region present that doesn’t seem to be dependent on the number of line segments drawn. This can be confirmed by the fact that $R(0) = 1$ and there is always going to one region present before we consider any points on the circle. Then we potentially have $R'(n) = \binom{n}{2} + 1$. However when $n >= 3$ this pattern seems to break down. $R(4) = 8$ , $R(5) = 16$, and $R(6) = 31$ but we have the estimated values $R'(4) = 7$, $R'(5) = 11$ and $R'(6) = 16$. This difference that we observe between $R(n)$ and $R'(n)$ can be explained through the number of intersection between chords in the circle (convince yourself of this). We have an intersection between chords for every two lines, which require $4$ points so there are a total of $\binom{n}{4}$ intersections for $n$ points. Then $R(n) = \binom{n}{2} + \binom{n}{4} + 1$ (you can check that adding $\binom{n}{4}$ doesn’t break any of the smaller cases). For a proof of why $\binom{n}{2} + \binom{n}{4} + 1 = 2^{n-1}$ for $n \in [1,5]$, see the top comment on this Stack Exchange post.

Problem 2. You are given a 100-sided die. After you roll once, you can choose to either get paid the dollar amount of that roll OR pay one dollar for one more roll. What is the expected value of the game? Solution. Let $X$ be the payout from playing this game. For this approach I’m assuming that I’ll want to stop playing the game once I reach some value $x\in [1,100]$ and find the value of $x$ that maximizes $\mathbb{E}[X]$. In my opinion, this approach is flawed as we aren’t keeping track of the amount of money we’ve already paid which prevents us from maximizing profit, but this might be subverted by the fact that we’re calculating the EV of the game overall. So our strategy is to keep our winnings if we roll $X > x$ and and keep rerolling if we get $X\leq x$. An interesting thing to note is that since each roll of the dice is independent, each $n^\text{th}$ roll of the dice has exactly the same conditions and distribution as the first roll (except we’ve spent $n$ dollars). Then on our first roll we have one of two cases:
$1$: we roll $X> x$ with probability $\frac{100 - x}{100}$ with expected winning $\frac{101 + x}{2}$
$2$: we roll $X\leq x$ with probability $\frac{x}{100}$ and we pay $\$1$ to reroll for payout $\mathbb{E}[X] - 1$
Combining these two, we have

We can then differentiate to find the maximum:

Solving for $x$ gives us $x\approx 85.86$. Since $x$ can only take on discrete values, we check $85$ and $86$ to find that $\mathbb{E}[85] = 87.33$ and $\mathbb{E}[86] = 87.36$. Then, the expected value of the game optimized by using this strategy is $\$87.36$.

Problem 3. Suppose two players are playing a game. The first player chose an integer between 1-30. The second player picks a different one. After that, a random integer (x) between 1-30 will be generated. The player whose number is closer to x get paid x dollars. Would you go first or second? What number should you pick? Solution. Let $m$ and $n$ be Player 1 and Player 2’s choices respectively. Player 2 can maximize his payout by choosing $n$ to be close to $m$ but he must decide whether it is optimal to choose above or below Player 1’s choice. In order for Player 2 to choose above Player 1, then expected value of choosing higher than $n$ must be greater than the expected value of choosing lower than $n$, that is

Then, should Player 1 choose $n \leq 21$, then Player 2 would choose $m= n+1$ and if Player 1 chose $n\geq 22$ Player 2 would choose $m=n-1$. The expected value is clearly maximized at either $n=21$ or $n=22$ for Player 1, and a quick calculation finds that $\mathbb{E}[21] = \frac{77}{10}$ and $\mathbb{E}[22] = \frac{78}{10}$. Then Player $1$ would choose $22$ and Player 2 would choose $21$. Since Player 1’s expected payoff is slightly higher than that of Player $2$, I would choose to go first and pick $n=22$.

Problem 4. A survey is given to all passengers on a number of different planes. The survey asks each person how full their plane was. The people answer honestly. If 50% of people claim that their plane was 80% full, while the other 50% claim that their plane was 20% full, how full was the average plane? Solution. This is a relatively simple question that’s intuitively misleading. An incorrect approach to the question would be to average out the $20\%$ and the $80\%$ passengers for a total of $50\%$ fullness on plans on average. Instead note that since the total number of people that claim $80\%$ of the plane is full is equal to the total number of people who claim their plane is $20\%$ full, there must be more planes carrying people at $20\%$ capacity than at $80\%$. In fact, there are $4$ times as many people in planes $20\%$ full as there are peope in planes $80\%$ full. Then, the average capacity of each plane is

Note that the first approach is wrong since averaging out the percentages assumes that the total number of people flying in each type of plane is distributed uniformly across the proportions of plane capacity. You can find this question on Jane Street’s Glassdoor.

Extra Problems

Problem. Given an array of length $n$ find the largest possible sum of consecutive elements of the array. Solution. This question is one of the classic dp questions from Brian Dean’s academic site. Clearly, the max sum will be along a subarray that is completely positive, so we need only keep track of the positive elements. We can then use a sliding window technique: keep track of the maximum sum up to a certain index $j$ and decide whether to add the next element based on how big it is compared to the existing sub-array. Along the way, we can update the overall maxSum by comparing the current maxSum to the sum of the subarray being considered.

int maxContiguousSum(int arr[], int n){
    int maxSum = arr[0];
    int maxSub = arr[0];

    for(int i = 1; i < n; i++){
        maxSub = max(arr[i], maxSub + arr[i]);
        maxSum = max(maxSum, maxSub);
    }

    return maxSum;
}

This solution runs in $O(n)$ time.

Problem. We randomly sample from a uniform distribution on $[0,1]$ until the sum of all sampled values exceeds $1$. What is the expected number of samples we take? Solution. Let $N$ be the number of samples we take and sum together to get a number greater than $1$. We would like to find $P(N = n) \geq 0$ since $N$ is a discrete random variable. We can find this by taking $P(N \leq n) - P(N < n) = P(N \leq n) - P(N \leq n-1)$, or equivalently $P(N > n - 1) - P(N > n)$. Note that $P(N > n)$ means that it takes more than $n$ samples to sum up to $1$, or equivalently that the first $n$ uniform r.v.’s that we draw sum up to less than $1$. The probability of this occuring is simply $\frac{1}{n!}$, as shown on Day 5 Problem 5. Then, we have

where $n = 1, 2, 3, \dots$ We can use the definition of expected value to solve for the expected number of samples we need to take:

Then we expect to draw $e$ times in order for the sum to exceed $1$.